<영의 간섭>
빛의 본성이 파동일 것이라는 예측을 직접 확인시켜주는 최초의 실험이 1801년 영(T.Young)에 의해 이루어 졌다. 영의 이중슬릿 간섭 실험은 빛이 파동이라는 것을 밝혀 주었을 뿐만 아니라 그 파장까지도 측정한 점에서 역사적 의미가 크다.
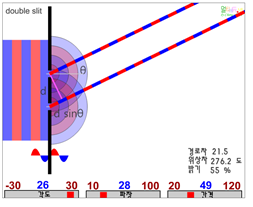
이중슬릿 간섭의 원리_ 입사한 평면파가 두 슬릿(실틈)에 입사하여 각 슬릿에서부터 구면파로 퍼져나간다. 이때 특정한 θ 방향의 먼 지점에서 만나게 될 두 파동의 위상관계를 살펴보면 두 파동이 합성되어서 어떤 밝기를 하게 될지를 계산할 수 있다.
위 그림에서 θ 기울어진 방향으로 나아가는 빛 두 줄기는 슬릿을 통과하는 순간의 위상은 서로 같았으나 멀리 떨어진 스크린의 같은 지점에 도달하게 되었을 때에는 각각이 달려온 거리가 달라서 서로 위상 차이가 생기게 된다.
위상은 α−k (빛의 경로) +ϵ 임으로 두 파의 위상차이는 k× (경로차) 가 될 것이다.
따라서 이 위상차이를 파장으로 표현하면,
Δα=kΛ=2πλdsinθ
여기서 Λ는 경로차이이다. 위상차는 두 광선이 향하는 방향각 θ가 0에서 점차 커지면 위상 차이도 0에서 점차 커져서 π/2 (90o), π (180o), 3π/2 (270o), 2π (360o), 4π (720o) 등으로 변화되고, 이에 따라 합성된 광선의 진폭도 커졌다 작아졌다 할 것이다.
아래 그림에서 위상차의 변화에 따라서 동일한 크기의 두 위상자가 합성된 결과를 그 값과 함께 보여준다.
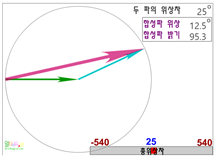
이중슬릿 간섭의 위상자 덧셈법_ 이중슬릿의 두 틈에서 나온 빛의 위상자와 이 두 위상자의 위상차이에 따른 합성 위상자를 붉은 색의 화살로 보여주고 있다. 두 위상자는 그 크기가 같으나 스크린에서의 위치에 따라서 위상차이가 생기고 이에 따라 합성된 위상자도 그림에서의 원호를 그리면서 달라진다. 이 위상차는 화면 오른편 아래의 슬라이더로 변경할 수 있다. 위상차 값이 2π(360o)를 주기로 하여 같은 결과가 거듭된다. 따라서 스크린에서의 밝기 분포도 주기적으로 거듭되는 것을 예상할 수 있다.
_ 위상자_ 구면파_ 평면파_ 파동_ 주기_ 간섭_ 진폭_ 슬릿_ 광선
<이중슬릿 간섭의 해석>
앞에서 위상자 방법으로 이중슬릿 간섭의 결과를 간단하게 예측해 볼 수 있었다. 이 경우 위상차 값이 2π 를 주기로 하여 합성된 결과가 같은 형태로 거듭되어 스크린 상에서 밝고 어두운 무늬가 계속해서 나타나는 것을 알 수 있다. 이것이 빛의 회절무늬와는 다른 특징이 된다. (실제로 빛의 가간섭 길이의 효과 때문에 스크린의 중앙에서 벗어나 경로차이가 가간섭 길이보다 커지면 간섭성이 떨어지게 되고 이에 따라 간섭무늬는 가장자리로 가면 밝고 어두운 무늬의 차이가 줄어들어 무늬가 희미해지게 된다)
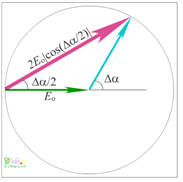
이중슬릿 간섭의 합성 위상자_ 위상차가 Δα일 때 두 위상자가 합성된 위상자는 그 크기가 2E0|cos(Δα/2)|이다.
위상차가 Δα일 때 두 위상자가 합성된 결과는 위 그림에서 보듯이 수평선에서 Δα/2 기울어져 있다. 따라서 이중슬릿의 한 틈으로 나온 빛의 진폭을 E0라 한다면 합성 위상자의 크기, 즉 진폭은 2E0|cos(Δα/2)|가 된다. 따라서 빛의 밝기를 위상차가 없는 중앙에서의 밝기 I0I0로 표시하면
I(θ)=I0cos2(Δα/2)=I0cos2(πλdsinθ)
만일에 슬릿에서 스크린까지의 거리(s)가 멀고, 스크린의 중앙에서 무늬까지의 거리(y)가 가까워서 θ≈ys가 거의 0에 가깝다면 위 식에서 sin(θ)≈θ로 놓을 수 있어,
I(y)=I0cos2πdyλs
다음 그림에서 보듯이 밝기의 분포는 Δy=sdλ의 간격으로 같은 형태가 거듭되고 있다.
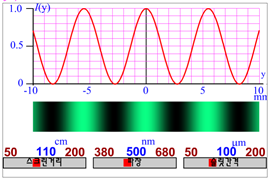
이중슬릿 간섭무늬와 그래프_슬릿간격, 파장, 스크린까지의 거리를 변화시킬 때의 간섭무늬 모양과 그래프를 나타내고 있다. 한편 그래프 위를 마우스로 클릭하면 함수의 값을 보여준다. 여기서는 실제의 이중슬릿 간섭에서의 상황을 나타내기 위하여 파장은 nm, 스크린까지의 거리는 cm, 슬릿간격은 μm, 스크린 위에서의 무늬는 mm를 단위로 하여 나타내었다.
위 그림에서 이중슬릿 간섭 조건을 바꾸어 가면서 무늬의 형태를 관찰해 보자. 이를 통해서 간섭이나 회절의 다음과 같은 특징을 알 수 있을 것이다.
파장이 줄어들면 무늬의 규모가 작아진다.
슬릿, 즉 창의 규모가 줄어들면 무늬의 규모가 커진다.
스크린까지의 거리가 늘어나면 무늬의 규모가 커진다.